サーボモータを指定した角度になるように制御します。常にサーボモータの仕様に合わせた時間管理が求められるリアルタイム制御です。
◀ この記事の前に： サーボモータ（ 設計・全体像 ）
▶ この記事の次に： サーボモータのリアルタイム制御（ タイマ割り込み ）
角度と ONデューティの関係
サーボモータの角度と ONデューティの関係を明確にします。ここで角度を時間として表すことができるようになります。プログラムの設計は時間を対象として行うことになります。
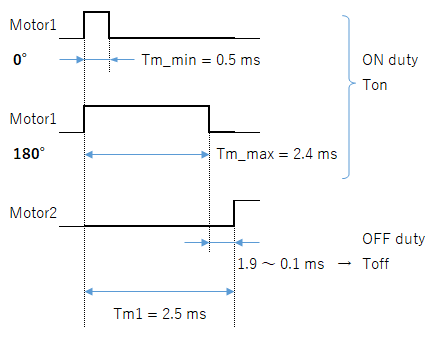
| 動作周波数： （ 周期 ） | fm Tm | 50 Hz 20 ms = 1 / fm |
| 動作角度： | θm_min θm_max | 0° 180° |
| ON デューティ： | Ton_min Ton_max | 0.5 ms 2.4 ms |
| モータ数（ 軸数 ）： | Nm | 7 |
角度と ONデューティの関係は以下のとおりです。
Tx = (( Tm_max – Tm_min ) / 180 ) X θx + Tm_min
θx： 軸の角度（ °）
Tx： ON デューティ
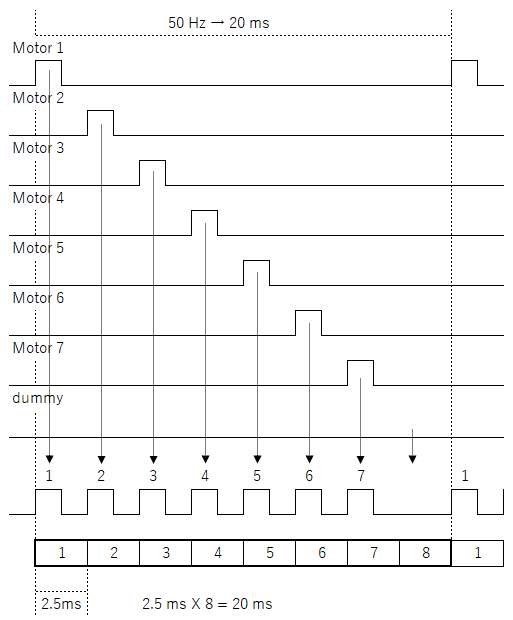
分散した場合のタイミングを検討
処理と出力を分散する場合のタイミングを検討します。７軸あるサーボモータを順番に処理と出力すれば分散することができます。個々のサーボモータの動作タイミングと比較して問題の有無を確認します。
各サーボモータを順番に処理と出力をおこなう
サーボモータは Tm時間ごとに ONデューティの処理と出力をおこないます。Tm は 20 msです。
計算しやすくするために軸数 Nmを仮に 8にします。
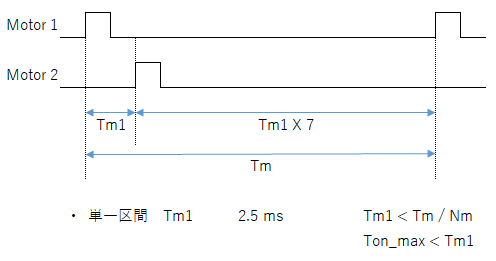
Tm1 = Tm / Nm
Tm1： ひとつのサーボモータあたりの時間
Tm1 は 2.5 msとなります。ON時間は 0.5 ms ～ 2.4 msですので Ton_max < Tm_one となります。
動作周波数の１サイクルを８分割しても、その分割した時間の中でサーボモータの ONデューティが収まることを意味しています。
角度の分解能
角度の分解能とはサーボモータの回転をきざむ角度です。分解能が 1°の場合は 1°ごとに角度を設定することができます。分解能が 0.1°の場合は 0.1°ごとに角度を設定することができます。分解能によってサーボモータの位置決め精度が決まります。
この角度の分解能はそのまま時間の分解能となります。サーボモータ制御はタイマ割り込みを使用して時間を管理します。タイマ割り込みのクロックが分解能となります。分解能を 1°にするためのクロック周波数を求めます。
角度が 0°～ 180°になるときの ONデューティは 0.5 ms ～ 2.4 msです。以下の式で計算できます。
( 2.4 – 0.5 ) / ( 180 – 0 ) = 10.56μs/deg.
1°あたりの ONデューティは 10.56μsになります。（ deg.は角度です。 ）
タイマのクロックを 10μsにすると分解能はほぼ 1°になります。そのときの 角度（ ONデューティ ）の最小値 0°と最大値 180°のタイマの値（ カウント数 ）は右記のとおりです。
分解能を 1°とした場合、タイマのクロックは 10μs
| ON デューティ | タイマ（カウント） | |
| Ton_min | 0.5 ms | 50 |
| Ton_max | 2.4 ms | 240 |
MCUのタイマ設定
MCUのタイマにこのクロックを供給する方法です。
MCUが STM32 でシステムクロックが 80 MHzの場合、プリスケーラで 1/800にすることにより 10 μsのクロックになります。
サーボモータの起動と停止に加減速を行う場合は、分解能が 1°では滑らかな制御ができません。分解能をさらに高める必要があります。
分解能を 10倍の 0.1°にする場合は、プリスケーラを 1/80にします。この場合、0.1°刻みの加減速が行うことができます。
タイマのクロックは多くの供給源から選択することができます。ここではシステムクロックにしました。プリスケーラはタイマの前段で分周を行いクロック周波数を変更する機能です。プリスケーラの値を変更することによりタイマの分解能を変更することができます。
リアルタイム制御は思いのほかに細かい時間が必要
Qumcum Lab. の動作に加減速を考慮した場合に必要な分解能は 0.1μs ～ 1μsになります。かなり細かい時間が必要になることが分かります。リアルタイム制御は外見的な動作の時間の裏には、もう一段階細かい時間が必要になる場合が少なくありません。
設計段階でこの時間スケールを押さえておかないと、完成後にカクカクした動きになってしまいます。タイマのクロックはシステムクロックに依存することが多いので、最悪 MCUの選定のし直しになります。ざっくりとで良いと思いますが、事前に机上で計算をしておくことをお薦めします。思いがけないバグを防ぐことができます。
実際の角速度
タイマの分解能が 10μsの場合、サーボモータの軸がどのくらいのスピード（ 角速度 ）で回転するか計算します。
サーボモータの角度は ONデューティにより決まりますので、時間当たりの ONデューティの増分が角速度になります。ONデューティの増分はタイマの分解能が限度になります。仮にサーボモータの制御周波数のサイクル（ 50 Hz、周期で 20 ms ）ごとにタイマのカウントひとつずつ増やすとした場合の計算を行います。１サイクルの時間と、１サイクルあたりの角度の変化が分かれば以下のとおり計算できます。
⊿θ / Tm
・⊿θ： １サイクルあたりの角度の変化
・Tm： サーボモータの制御周波数の周期
タイマを１カウント増やすということは ONデューティが 10μs増えると言うことです。10μsは角度に換算すると 0.95°になります。したがって ⊿θは 0.95°になります。
⊿θ = ( Ton_max – Ton_min ) / ( 180 – 0 ) × 10
Tmは 20 msですので以下のとおりです。秒速 約50°で、軸の端から端まで 180°の回転に要する時間は約 3秒になります。
⊿θ / Tm = 0.95°/ 20 ms = 47.5 deg./s
（ deg. は角度 ）
タイマのカウントの変化を１サイクルあたり２にすると約 100 deg./s、180°の回転は約２秒になります。
Technical Considerations 分解能が足りない
ONデューティの増減は制御サイクル（ 20 ms ）ごとにしか変更することができません。また、タイマのクロック分解能である 10μs単位でしか増加減することができません。分解能が 10μsの場合、秒速50°の次は秒速 100°です。この間の秒速 70°とか 80°にすることはできません。このままでは加速度を導入することが難しくなります。加速度は速度の変化です。速度を滑らかに変更できることが必要になります。
速度を滑らかに変更するためには、さらに速度の刻みを細かくする必要があります。そのためには、タイマの分解能を 10μsから 1μsや 0.1μsのように細かくする必要があります。可変割り込み方式を採用しているため、分解能を細かくしても処理の負荷が高くなることはありません。
プログラミングのための情報
プログラミングで必要となる情報は以下のとおりです。
サーボモータの仕様
| ・動作周波数： （ 周期 ） | fm Tm | 50 Hz 20 ms = 1 / fm |
| ・動作角度： | θm_min θm_max | 0° 180° |
| ・ON デューティ： | Ton_min Ton_max | 0.5 ms 2.4 ms |
| ・モータ数（ 軸数 ）： | Nm | 7 |
ONデューティの計算式
Tx = (( Tm_max – Tm_min ) / 180 ) X θx + Tm_min
θx： 軸の角度（ °）
Tx： ON デューティ
タイマのクロック
分解能が 1°の場合、10μs
STM32 システムクロック 80 MHz の場合、プリスケーラ値は 1/800
参考情報
他のサイトで参考になる情報は以下のとおりです。
このホームページ内
- 複数のMCUをつなぐ： このロボットには複数の MCUが搭載されています。その MCU間の接続の概要です。
他のWebサイト
- SN74LVC1G3157 SPDT アナログスイッチ Datasheet
